Measuring a Tennis Ball's Flatness from its Sound
A coworker told me about how the sound of a tennis ball’s drop can be used to determine whether the ball is flat or not. As one would expect, flatter balls don’t bounce as high as good balls, instead reaching a lower ratio of its initial drop height. This ratio can be computed from the sound of three successive bounce from some basic physics.
This notebook doesn’t actually determine if a ball is flat or not. It explores the variation in measurement of a single ball, which is all I had available.
import pydub
import matplotlib.pyplot as plt
def get_channels(audio):
# TODO consider using reshape
samples = audio.get_array_of_samples()
# odd samples
channel_0 = [samples[i] for i in range(0, len(samples), 2)]
# even samples
channel_1 = [samples[i] for i in range(1, len(samples), 2)]
return channel_0,channel_1
def index_to_time(i, frame_rate=44100):
"""return the time at which the i-th sample occurred"""
return i/frame_rate
def find_bounces(samples, threshold, frame_rate=44100, timeout=0.1):
retval = []
timeout_flag = False
time_last_sample = 0
time_current = 0
for i,sample in enumerate(samples):
time_current = index_to_time(i)
if timeout_flag and time_current > time_last_sample + timeout:
timeout_flag = False
if not timeout_flag and abs(sample)>threshold:
retval.append(time_current)
time_last_sample = time_current
timeout_flag = True
return retval
def compute_ratio(t_bounce):
print(f'\t{t_bounce[1] - t_bounce[0]}\t{t_bounce[2] - t_bounce[1]}')
ratio = ((t_bounce[2] - t_bounce[1])/(t_bounce[1] - t_bounce[0]))**2
#print(f'\t{ratio:2.3}')
return ratio
Read in the Data
The data is taken from dropping a tennis ball from various heights and recording the bounces from various heights:
ball[1-3].m4adropped from 3 feetball[4-6].m4adropped from 2 feet
audio = []
for i in range(6):
audio.append(pydub.AudioSegment.from_file(f'ball{i+1}.m4a'))
for i,a in enumerate(audio):
print(f'sample #{i}:\t{a.duration_seconds:2.2}\t{a.frame_rate}\t{a.channels}\t{a.sample_width}')
sample_duration = 1/audio[0].frame_rate
print(f'\nsamples are taken every {sample_duration:2.4} seconds = {sample_duration*10**6:2.4} us')
sample #0: 6.1 44100 2 2
sample #1: 4.0 44100 2 2
sample #2: 4.1 44100 2 2
sample #3: 3.6 44100 2 2
sample #4: 3.7 44100 2 2
sample #5: 4.4 44100 2 2
samples are taken every 2.268e-05 seconds = 22.68 us
Waveform Plots
Let’s plot the waveforms to understand them. The rows are the 6 samples, and each column is the channel of each audio sample.
It looks like we can capture the first three bounces by thresholding the absolute value of the data above 1000. We can come up with a better way of determining a threshold later.
# reference on subplots: https://realpython.com/python-matplotlib-guide/
fig, ax = plt.subplots(nrows=6, ncols=2, figsize=(16, 20))
for row,a in enumerate(audio):
channels = get_channels(a)
for col,channel in enumerate(channels):
x = range(len(channel))
y = channel
ax[row][col].plot(x,y)
ax[row][col].set_title(f'sample {row}, channel #{col}')
ax[row][col].set_xlim([0, 250000])
ax[row][col].set_ylim([-8000, 8000])
fig.tight_layout()
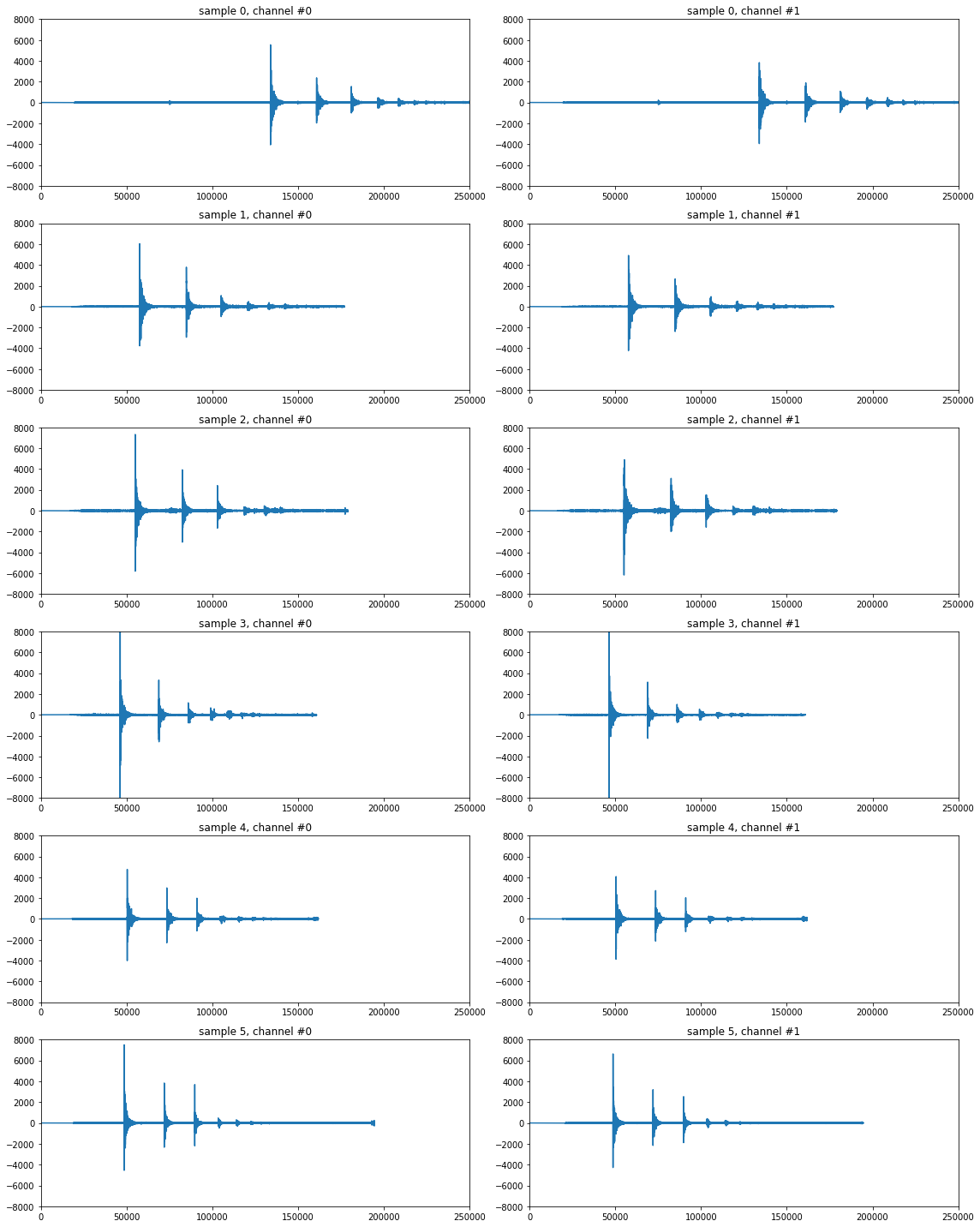
Sanity Check
As a sanity check, the number of samples multiplied by the sample duration should match the file duration, and it does.
for a in audio:
print(len(get_channels(a)[0])*sample_duration, a.duration_seconds)
6.106848072562358 6.106848072562358
4.017052154195011 4.017052154195011
4.063492063492063 4.063492063492063
3.645532879818594 3.645532879818594
3.6687528344671203 3.6687528344671203
4.4117913832199545 4.4117913832199545
Compute Airtime
The time, t, taken for a ball to fall is related to height, h, dropped by $h = \frac{gt^2}{2}$. Since a bounce consists of a trip up and down, this time needs to be doubled for the bounce time.
import math
def compute_air_time(h):
"""return time for a bounce"""
return 2*math.sqrt(2*h/9.8)
def compute_ratio(b):
return ((b[2] - b[1])/(b[1] - b[0]))**2
const_m_per_ft = 0.3048
for h in range(1, 8):
print(f'airtime for a max height bounce of {h}: {compute_air_time(h * const_m_per_ft):2.2} s')
airtime for a max height bounce of 1: 0.5 s
airtime for a max height bounce of 2: 0.71 s
airtime for a max height bounce of 3: 0.86 s
airtime for a max height bounce of 4: 1.0 s
airtime for a max height bounce of 5: 1.1 s
airtime for a max height bounce of 6: 1.2 s
airtime for a max height bounce of 7: 1.3 s
for i,a in enumerate(audio):
print(f'sample #{i}')
channels = get_channels(a)
t_bounce = find_bounces(channels[0], 1000)
print(f'\tratio = {compute_ratio(t_bounce):2.3}')
sample #0
ratio = 0.568
sample #1
ratio = 0.557
sample #2
ratio = 0.556
sample #3
ratio = 0.579
sample #4
ratio = 0.579
sample #5
ratio = 0.583